7. Ecuación de Schrödinger y sus soluciones

Esta ecuación fue formulada por Erwin Schrödinger en 1926, esta ecuación describe el comportamiento ondulatorio de las partículas en la mecánica cuántica.
Permite conocer cómo evoluciona la función de onda Ψ, que representa la probabilidad de encontrar una partícula en un lugar y momento determinados. 

Introducción

La ecuación de Schrödinger fue formulada en 1926 por el físico austríaco Erwin Schrödinger y constituye el pilar fundamental de la mecánica cuántica.
Su propósito es describir matemáticamente cómo cambia en el tiempo el estado cuántico de una partícula, como un electrón en un átomo. 

Schrödinger propuso que toda partícula puede describirse mediante una función de onda Ψ, que contiene toda la información física del sistema.
Esta función no indica una trayectoria como en la mecánica clásica, sino la probabilidad de encontrar la partícula en un determinado lugar del espacio. 

Ecuación de Schrödinger dependiente del tiempo

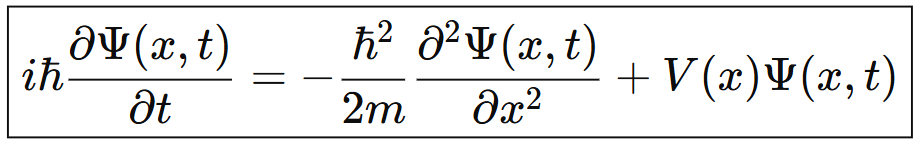
Esta ecuación permite conocer cómo evoluciona en el tiempo la función de onda Ψ de una partícula en una dimensión. 

Ecuación de Schrödinger independiente del tiempo

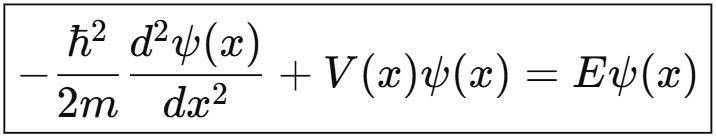
Resolver esta ecuación permite obtener los niveles de energía permitidos y las formas de los orbitales donde es más probable encontrar al electrón.

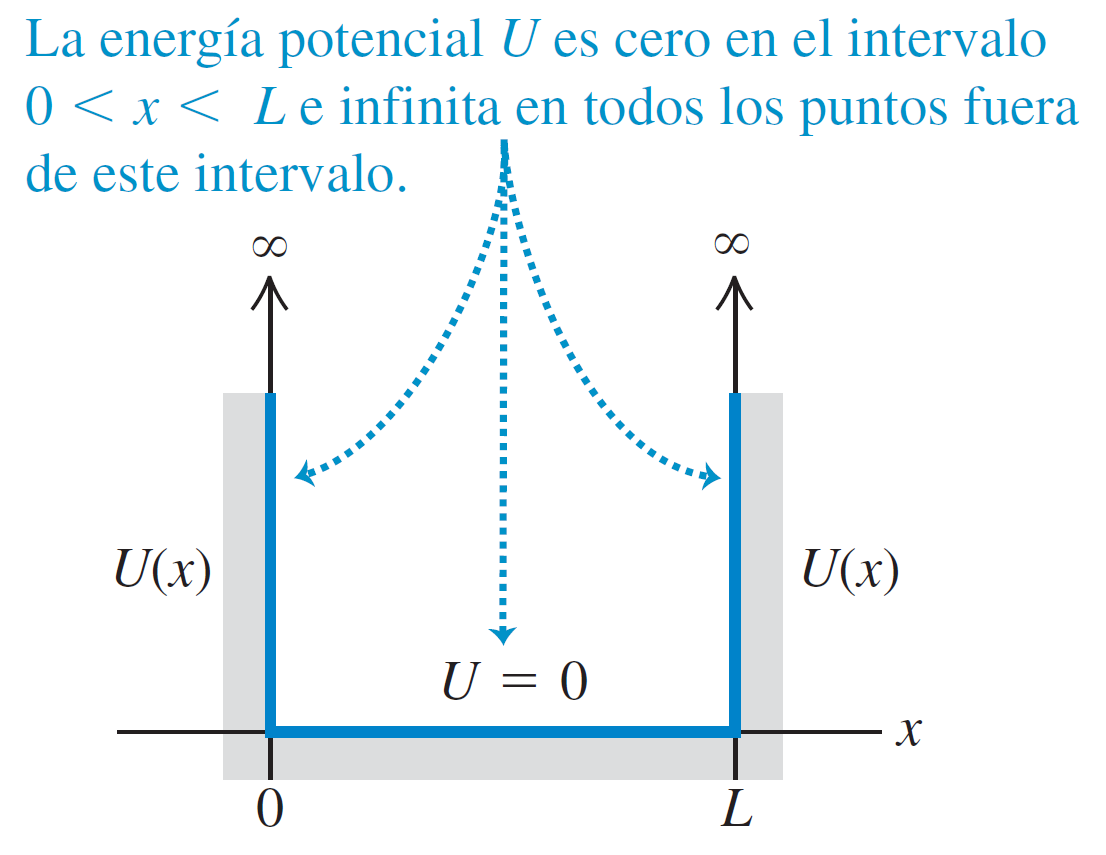
Partícula en una caja (pozo de potencial infinito)

Este es el modelo más sencillo para aplicar la ecuación de Schrödinger.
Se supone que una partícula de masa mmm está confinada en una región entre x=0 y x=L, donde el potencial V(x)=0, y fuera de esa región el potencial es infinito (V=∞), impidiendo que la partícula escape. 

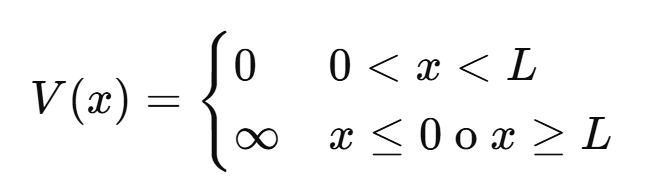
Ecuación de Schrödinger dentro de la caja: 

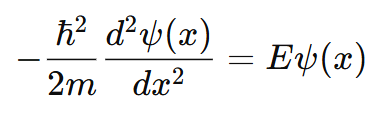
Solución general:

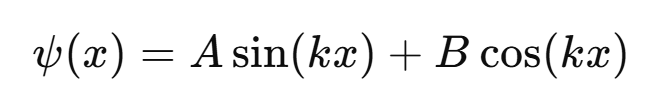
Los niveles de energía permitidos son:

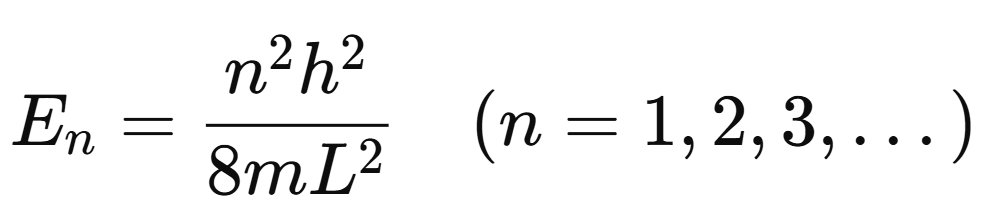
Pozo de potencial finito

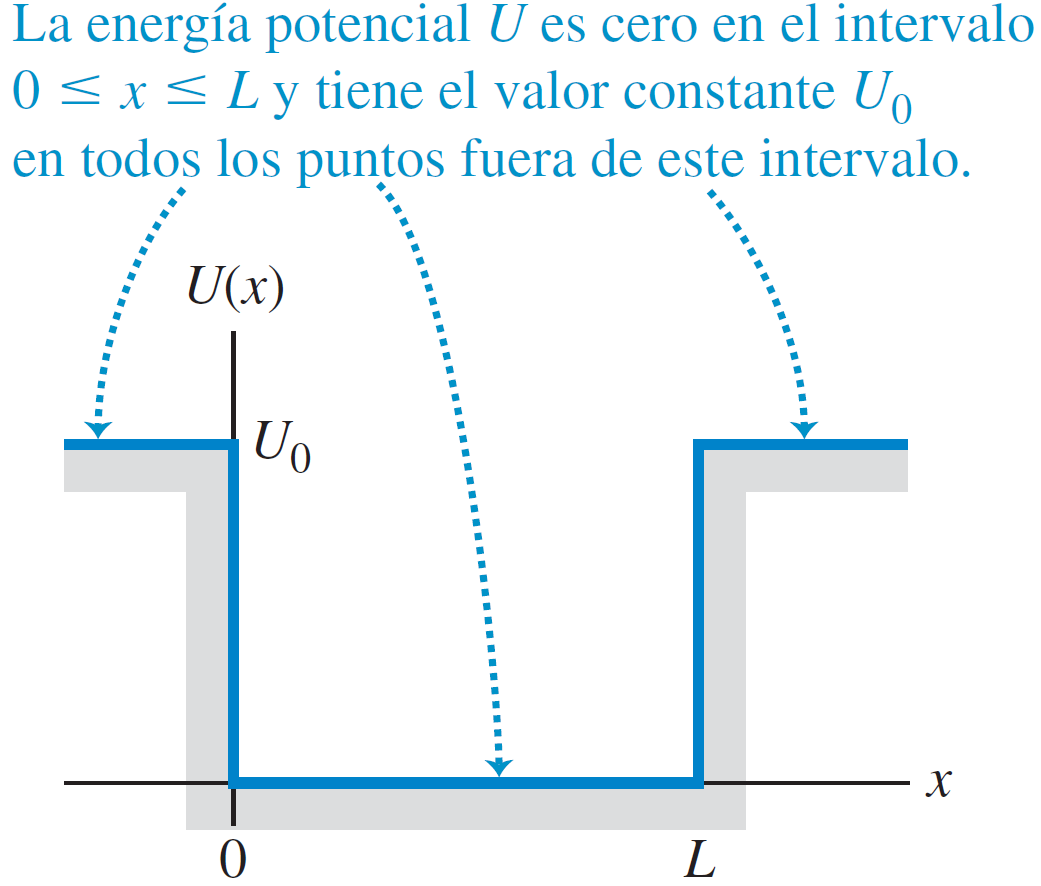
Ahora el potencial ya no es infinito fuera de la caja, sino que tiene un valor finito V0.
El sistema se representa como: 

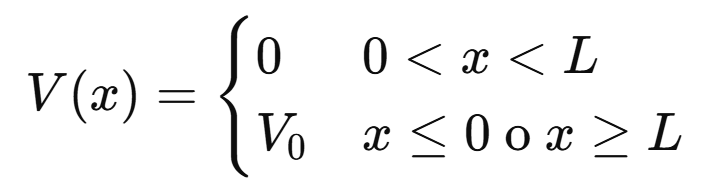
Solución a la ecuación:

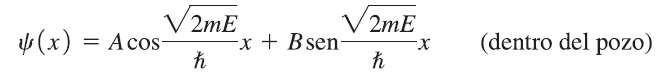
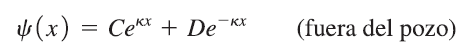
Barreras de potencial y tunelamiento

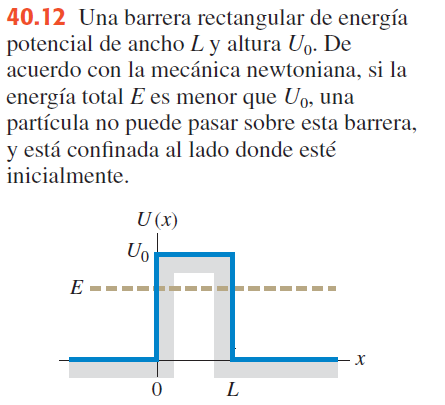
Una barrera de potencial es lo contrario a un pozo de potencial: es una función de energía potencial con un máximo.

En la mecánica clásica (newtoniana):

• Si una partícula tiene una energía total E1E_1E1​ menor que la altura de la barrera U(a), no puede superarla.

• En el punto donde U>EU > EU>E, la energía cinética K=E−U sería negativa, lo que implicaría una rapidez imaginaria o masa negativa, ambas imposibles.

• Solo si E>U0​, la partícula podría "pasar por encima" de la barrera, igual que un carrito de montaña rusa que tiene suficiente energía para remontar una subida.

Sin embargo, la mecánica cuántica introduce un comportamiento completamente distinto.
Debido a la naturaleza ondulatoria de las partículas, una partícula que se aproxima a una barrera de potencial no es siempre reflejada:
existe una probabilidad finita de que atraviese la barrera, aunque su energía sea menor que la altura de ésta.

A este fenómeno se le llama tunelamiento cuántico.
El término es una analogía: como si la partícula "abriera un túnel" a través de la montaña (la barrera) sin necesidad de subir hasta la cima.
No obstante, la partícula no perfora físicamente la barrera ni pierde energía al hacerlo; simplemente su función de onda se extiende a través de la región prohibida y puede continuar al otro lado.

Tunelamiento a través de una barrera rectangular

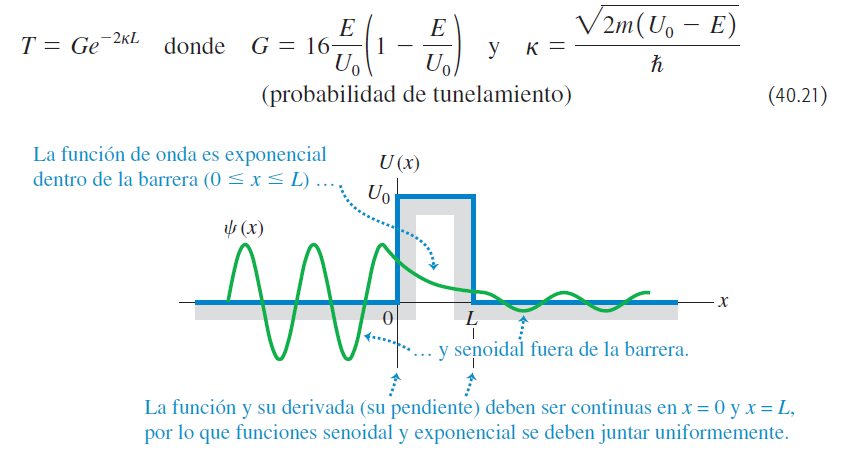
Aplicaciones del tunelamiento

1. Emisión alfa en núcleos radiactivos

En los átomos radiactivos, las partículas alfa (núcleos de helio) están atrapadas dentro del núcleo por una fuerte barrera de potencial nuclear.
Según la mecánica clásica, nunca podrían escapar, pero gracias al tunelamiento, existe una pequeña probabilidad de que salgan del núcleo, lo que explica la desintegración alfa y la vida media de los elementos radiactivos.

2. Fusión nuclear en las estrellas

En el Sol y en otras estrellas, los protones deben acercarse muchísimo para fusionarse, pero las fuerzas de repulsión eléctrica (Coulomb) entre ellos lo impiden clásicamente.
El tunelamiento cuántico permite que los protones se acerquen lo suficiente para que actúe la fuerza nuclear fuerte, haciendo posible la fusión nuclear que libera la energía del Sol.

3. Microscopio de efecto túnel (STM)

El microscopio de efecto túnel utiliza el tunelamiento de electrones para observar la superficie de materiales con resolución atómica.
Cuando una punta metálica muy afilada se aproxima a una superficie conductora, se produce una corriente de túnel que depende de la distancia entre ambos.
Al medir esta corriente, el STM puede "dibujar" los átomos individuales de una superficie.

4. Diodos y transistores túnel

En los semiconductores, el tunelamiento permite el paso de electrones a través de barreras de potencial muy delgadas.
Este principio se usa en:

• Diodos túnel, que presentan una región de resistencia negativa útil en osciladores y amplificadores.

• Transistores cuánticos, donde el efecto túnel controla el flujo de corriente en dispositivos a escala nanométrica.